To path indicator Subpages of “Research“ To navigation To quick access To footer with other services
To content
Logo of TRR 391
Students in summer on north campus, red gears in background. © Roland Baege​/​TU Dortmund
B01

Statistical modeling and analysis for state estimation in electrical power distribution grids

B01 addresses statistical challenges caused by the integration of renewable energies and the dismantling of conventional power plants with simultaneous electrification of heating and transport sectors. It develops methods for data acquisition and monitoring to design smart distribution grids. In the long run, new experimental designs for nonlinear state space models and new monitoring procedures will be developed for the optimal resilient and robust operation of electrical power distribution grids.

Project Leaders

Prof. Dr. Christine Müller
Department of Statistics -Chair of Statistics with Applications in Engineering Sciences
TU Dortmund University

Prof. Dr.-Ing. Christian Rehtanz
Department of Electrical Engineering and Information Technology - Institute of Energy Systems, Energy Efficiency and Energy Economics
TU Dortmund University

Summary

Integrating renewable energy conversion systems and dismantling conventional power plants, while simultaneously electrifying the heating and transport sectors, creates new challenges in the planning and operation of electrical power distribution grids. A key functionality for efficient grid operation and usage is the estimation and prediction of the operational states in terms of voltages and power flows.

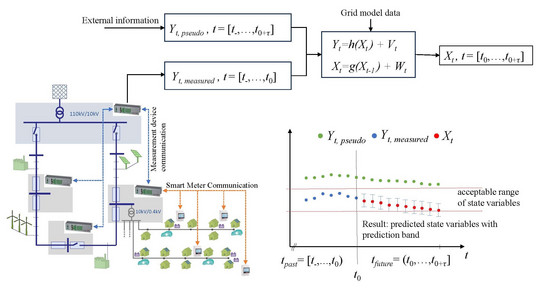
Classical state estimation techniques currently in use estimate the state variables at a single point in time. This is achieved by utilizing a sufficiently large number of measurements of spatially distributed sensors, which are time-synchronized within certain limits, and assuming a steady-state behavior of the measured values in a specific time interval of several seconds. However, in distribution grids, the number of spatially distributed sensors is significantly lower in comparison to transmission grids, where state estimation are ubiquitous in use. The measurements on distribution level have typically a lower temporal resolution and the steady-state assumption significantly reduces accuracy due to the high volatility of loads and feed-ins. Additionally, due to the limited number of measurements at sensors, less accurate pseudo-measurement values must be incorporated to achieve observability. Such pseudo-measurements are values derived from secondary data replacing a missing measurement. They are for instance obtained from weather reports to get the electrical input of wind power plants or photovoltaic systems, which might not be measured directly.

The first objective of this project is to design new methods which incorporate the temporal evolution of measured values and the formation of pseudo-measured values, as well as the spatial distribution of measurements, including correlations, into the estimation process. We will achieve this goal by determining important input variables, employing realistic model assumptions, and developing appropriate filtering methods. Specifically, we will relax the common normality assumption, which is unrealistic for electrical power distribution grids. This will lead us to new statistical approaches for the nonlinear state space models typically used in distribution grids, enabling robust estimation under highly volatile conditions.

Furthermore, on the distribution grid level, we need to ensure that voltage or power flows are kept within defined values with a specific confidence level for specific future time intervals. Therefore, our second goal is to determine the prediction intervals (confidence intervals) for the predicted (estimated) future values over a short time interval (e.g., 15 minutes) and to develop online change-point methods for detecting critical situations where the voltage or power flow will exceed critical values in the upcoming time interval. Expanding this time interval from short-term to daily operation is the long-term goal of the project.

To guarantee the required accuracy and probability, an optimal mix of sensors and different types of pseudo-measurements needs to be determined, and we will identify the minimum number of sensor measurements and their placement in medium and low-voltage networks.  Additionally, we will determine optimal estimation intervals for the required accuracy. In a further step, the topology of the underlying grid model will be validated. Changes in the grid topology lead to modeling errors, which provide significant practical problems in today's analysis of distribution grids. To address these issues, we will develop new online change-point methods for detecting changes in the network topology that were not communicated to the network operator in a timely manner.

Abbas, S., R. Fried, J. Heinrich, M. Horn, et al. (2019). Detection of anomalous sequences in crack data of a bridge monitoring. Applications in Statistical Computing — From Music Data Analysis to Industrial Quality Improvement. Eds. K. Ickstadt, H. Trautmann, G. Szepannek, N. Bauer, K. Lübke, M. Vichi. Springer, 251–269. doi: 10.1007/978-3-030-25147-5_16.

Abur, A. and A. Gomez-Exposito (2004). Power System State Estimation: Theory and Implementation. Marcel Dekker, New York. doi: 10.1201/9780203913673.

Adler, D. and D. Murdoch (2020). rgl: 3D Visualization Using OpenGL. url: https://CRAN.R-project.org/package=rgl.

Afshar, S., K. Morris, and A. Khajepour (2019). A modified sliding-mode observer design with application to diffusion equation. International Journal of Control 92, 2369–2382. doi: 10.1080/00207179.2018.1438668.

Balduin, S., E. M. Veith, A. Berezin, S. Lehnhoff, et al. (2021). Towards a universally applicable neural state estimation through transfer learning. 2021 IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), 1–6. doi: 10.1109/ISGTEurope52324.2021.9639919.

Brodsky, B. (2012). Sequential change-point detection in state-space models. Sequential Analysis 31, 145–171. doi: 10.1080/07474946.2012.665676.

Brüggemann, A., K. Görner, and C. Rehtanz (2017). Evaluation of extended Kalman filter and particle filter approaches for quasi-dynamic distribution system state estimation. CIRED - Open Access Proceedings Journal 2017, 1755–1758. doi: 10.1049/oap-cired.2017.0984.

Brüggemann, A., C. Rehtanz, and T. Noll (2019). Analysis of State Uncertainty for Distribution System State Estimation. 2019 IEEE Milan PowerTech. Milan, Italy: IEEE, 1–6. doi: 10.1109/PTC.2019.8810800.

Brüning Ascari, L. and A. Somoes Costa (2023). A bad data resilient multisensor fusion framework for hybrid state estimation. IEEE Powertech 2023. doi: 10.1109/TPWRS.2023.3261201.

Calvet, L. E., V. Czellar, and E. Ronchetti (2015). Robust Filtering. Journal of the American Statistical Association 110, 1591–1606. doi: 10.1080/01621459.2014.983520.

Cao, M., J. Guo, H. Xiao, and L. Wu (2022). Reliability analysis and optimal generator allocation and protection strategy of a non-repairable power grid system. Reliability Engineering & System Safety 222, 108443. doi: 10.1016/j.ress.2022.108443.

Cipra, T. and R. Romera (1997). Kalman filter with outliers and missing observations. TEST: An Official Journal of the Spanish Society of Statistics and Operations Research 6, 379–395. doi: 10.1007/BF02564705.

Creal, D. D. and R. S. Tsay (2015). High dimensional dynamic stochastic copula models. Journal of Econometrics 189, 335–345. doi: 10.1016/j.jeconom.2015.03.027.

Crevits, R. and C. Croux (n.d.). Robust Estimation of Linear State Space Models (). doi: 10.2139/ssrn.3068633.

Dovoedo, Y. H. and S. Chakraborti (2016). On the robustness to symmetry of some nonparametric multivariate one-sample sign-type tests. Journal of Statistical Computation and Simulation 86, 1936–1953. doi: 10.1080/00949655.2015.1092540.

Du, X., A. Engelmann, Y. Jiang, T. Faulwasser, et al. (2020). Optimal experiment design for AC power systems admittance estimation. IFAC-PapersOnLine 53, 13311–13316. doi: 10.1016/j.ifacol.2020.12.163.

Duan, P., L. He, L. Huang, G. Chen, et al. (2022). Sensor scheduling design for complex networks under a distributed state estimation framework. Automatica 146, 110628. doi: 10.1016/j.automatica.2022.110628.

Dyckerhoff, R., C. Ley, and D. Paindaveine (2015). Depth-based runs tests for bivariate central symmetry. Annals of the Institute of Statistical Mathematics 67, 917–941. doi: 10.1007/s10463-014-0480-y.

Echternacht, D. (2015). Optimierte Positionierung von Messtechnik zur Zustandsschätzung in Verteilnetzen. PhD Thesis. Aachen: Printproduction. url: https://publications.rwth-aachen.de/record/478587.

Fan, Y. R., G. H. Huang, B. W. Baetz, Y. P. Li, et al. (2017). Development of a copula-based particle filter (CopPF) approach for hydrologic data assimilation under consideration of parameter interdependence. Water Resources Research 53, 4850–4875. doi: 10.1002/2016WR020144.

Flossdorf, J., R. Fried, and C. Jentsch (2023). Online monitoring of dynamic networks using flexible multivariate control charts. Social Network Analysis and Mining 13, 489–502. doi: 10.1007/s13278-023-01091-y.

Flossdorf, J. and C. Jentsch (2021). Change detection in dynamic networks using network characteristics. IEEE Transactions on Signal and Information Processing over Networks 7, 451–464. doi: 10.1109/TSIPN.2021.3094900.

Harvey, A. and A. Luati (2014). Filtering With Heavy Tails. Journal of the American Statistical Association 109, 1112–1122. doi: 10.1080/01621459.2014.887011.

Hermann, S., K. Ickstadt, and C. H. Müller (2016). Bayesian prediction of crack growth based on a hierarchical diffusion model. Applied Stochastic Models in Business and Industry 32, 494–510. doi: 10.1002/asmb.2175.

Hermann, S., K. Ickstadt, and C. H. Müller (2018). Bayesian prediction for a jump diffusion process – With application to crack growth in fatigue experiments. Reliability Engineering & System Safety 179, 83–96. doi: 10.1016/j.ress.2016.08.012.

Hilbrich, D., S. Raczka, and C. Rehtanz (2022). Optimized grid reduction for state estimation algorithms in under-determined distribution grids. NEIS 2022; Conference on Sustainable Energy Supply and Energy Storage Systems, 1–6. url: https://ieeexplore.ieee.org/document/10048082.

Horn, M. and C. H. Müller (2023). Sign depth tests in multiple regression. Journal of Statistical Computation and Simulation 93, 1169–1191. doi: 10.1080/00949655.2022.2130922.

Huang, Y., Y. Zhang, Y. Zhao, and J. A. Chambers (2019). A Novel Robust Gaussian–Student’s t Mixture Distribution Based Kalman Filter. 67, 3606–3620. doi: 10.1109/TSP.2019.2916755.

Iacus, S. (2008). Simulation and Inference for Stochastic Differential Equations. Springer, New York. url: https://link.springer.com/book/10.1007/978-0-387-75839-8.

Ivanov, E., A. Min, and F. Ramsauer (2017). Copula-based factor models for multivariate asset returns. Econometrics 5. doi: 10.3390/econometrics5020020.

Kennedy, J. and R. Eberhart (1995). Particle swarm optimization. Proceedings of ICNN’95 — International Conference on Neural Networks. Vol. 4. IEEE, 1942–1948.

Klein, D., L. Hackstein, S. Stütz, and C. Rehtanz (2017). An integrated optimization approach for multi-voltage level network expansion planning. 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe, 923–928. url: http://ieeexplore.ieee.org/xpl/mostRecentIssue.jsp?punumber=8246021.

Kloubert, M.-L. and C. Rehtanz (2018). Probabilistic Load Flow Method for Correlated Multimodally Distributed Input Variables. 2018 Power Systems Computation Conference (PSCC). Dublin, Ireland: IEEE, 1–6. doi: 10.23919/PSCC.2018.8442451.

Kreuzer, A., L. Dalla Valle, and C. Czado (2022). A Bayesian non-linear state space copula model for air pollution in Beijing. Journal of the Royal Statistical Society Series C: Applied Statistics 71, 613–638. doi: 10.1111/rssc.12548.

Kreuzer, A., L. D. Valle, and C. Czado (2023). Bayesian multivariate nonlinear state space copula models. Computational Statistics & Data Analysis, 107820. doi: 10.1016/j.csda.2023.107820.

Kustosz, C. P., A. Leucht, and C. H. Müller (2016a). Tests Based on Simplicial Depth for AR(1) Models With Explosion. Journal of Time Series Analysis 37, 763–784. doi: 10.1111/jtsa.12186.

Kustosz, C. P., C. H. Müller, and M. Wendler (2016b). Simplified simplicial depth for regression and autoregressive growth processes. Journal of Statistical Planning and Inference 173, 125–146. doi: 10.1016/j.jspi.2016.01.005.

Lambrichts, W. and M. Paolone (2023). Experimental validation of a unified and linear state estimation method for hybrid AC/DC microgrids. IEEE Powertech 2023. doi: 10.1109/PowerTech55446.2023.10202917.

Leckey, K., D. Malcherczyk, M. Horn, and C. H. Müller (2023). Simple powerful robust tests based on sign depth. Statistical Papers 64, 857–882. doi: 10.1007/s00362-022-01337-5.

Leckey, K., C. H. Müller, S. Szugat, and R. Maurer (2020). Prediction intervals for load-sharing systems in accelerated life testing. Quality and Reliability Engineering International 36, 1895–1915. doi: 10.1002/qre.2664.

Li, Q., R. Negi, and M. D. Ilić (2011). Phasor measurement units placement for power system state estimation: A greedy approach. 2011 IEEE Power and Energy Society General Meeting, 1–8. doi: 10.1109/PES.2011.6039076.

Malcherczyk, D., K. Leckey, and C. H. Müller (2021). K-sign depth: From asymptotics to efficient implementation. Journal of Statistical Planning and Inference 215, 344–355. doi: 10.1016/j.jspi.2021.04.006.

Malevich, N. and C. H. Müller (2019). Optimal design of inspection times for interval censoring. Statistical Papers 60, 449–464. doi: 10.1007/s00362-018-01067-7.

Malevich, N., C. H. Müller, J. Dreier, M. Kansteiner, et al. (2021). Experimental and statistical analysis of the wear of diamond impregnated tools. Wear 468–469, 203574. doi: 10.1016/j.wear.2020.203574.

Marczak, M., T. Proietti, and S. Grassi (2017). A data-cleaning augmented Kalman filter for robust estimation of state space models. Econometrics and Statistics 5, 2452–3062. doi: 10.1016/j.ecosta.2017.02.002.

Meinecke, S., D. Sarajlić, S. R. Drauz, A. Klettke, et al. (2020). SimBench—A Benchmark Dataset of Electric Power Systems to Compare Innovative Solutions Based on Power Flow Analysis. Energies 13, 3290. doi: 10.3390/en13123290.

Mestav, K. R., J. Luengo-Rozas, and L. Tong (2019). Bayesian state estimation for unobservable distribution systems via deep learning. IEEE Transactions on Power Systems 34, 4910–4920. doi: 10.1109/TPWRS.2019.2919157.

Moradi, M., H. Amindavar, and J. A. Ritcey (2017). Copula-based particle filtering for target tracking in non-linear/non-Gaussian scenarios with correlated sensors. 2017 IEEE Radar Conference (RadarConf). Seattle, WA, USA: IEEE, 0651–0656. doi: 10.1109/RADAR.2017.7944284.

Möttönen, J. and H. Oja (1995). Multivariate spatial sign and rank methods. Journal of Nonparametric Statistics 5, 201–213. doi: 10.1080/10485259508832643.

Müller, C. and K. Schorning (2023). A-optimal designs for state estimation in networks. Statistical Papers 64, 1159–1186. doi: 10.1007/s00362-023-01435-y.

Müller, C. H. and S. H. Meinke (2018). Trimmed likelihood estimators for stochastic differential equations with an application to crack growth analysis from photos. doi: 10.5445/KSP/1000083488/01.

Müller, C. H. and R. Meyer (2022). Inference of intensity-based models for load-sharing systems with damage accumulation. IEEE Transactions on Reliability 71, 539–554. doi: 10.1109/TR.2022.3140483.

Muscas, C., M. Pau, P. A. Pegoraro, and S. Sulis (2014). Effects of measurements and pseudomeasurements correlation in distribution system state estimation. IEEE Transactions on Instrumentation and Measurement 63, 2813–2823. doi: 10.1109/TIM.2014.2318391.

Nicolicioiu, A., I. Duta, and M. Leordeanu (2019). Recurrent Space-time Graph Neural Networks. arXiv. url: http://arxiv.org/abs/1904.05582.

Paindaveine, D. (2009). On multivariate runs tests for randomness. Journal of the American Statistical Association 104, 1525–1538. doi: 10.1198/jasa.2009.tm09047.

Pegoraro, P. A., A. Angioni, M. Pau, A. Monti, et al. (2017). Bayesian approach for distribution system state estimation with non-Gaussian uncertainty models. IEEE Transactions on Instrumentation and Measurement 66, 2957–2966. doi: 10.1109/TIM.2017.2728398.

Ruckdeschel, P., B. Spangl, and D. Pupashenko (2014). Robust Kalman tracking and smoothing with propagating and non-propagating outliers. Statistical Papers 55, 93–123. doi: 10.1007/s00362-012-0496-4.

Schlemminger, M., T. Ohrdes, E. Schneider, and M. Knoop (2022). Dataset on electrical single-family house and heat pump load profiles in Germany. Scientific Data 9, 56. doi: 10.1038/s41597-022-01156-1.

Schlösser, T., A. Angioni, F. Ponci, and A. Monti (2014). Impact of pseudo-measurements from new load profiles on state estimation in distribution grids. 2014 IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Proceedings, 625–630. doi: 10.1109/I2MTC.2014.6860819.

Schurtz, A. (2020). Verfahren zur Zustandsschätzung und ihr Beitrag zum Engpassmanagement in Mittelspannungsnetzen. Dissertation, TU Dortmund, Dortmunder Beiträge zu Energiesystemen, Energieeffizienz und Energiewirtschaft, Shaker-Verlag.

Schwierz, T., S. Raczka, D. Hilbrich, and C. Rehtanz (2022). Development of a measurement-based algorithm for topology detection in distribution grids. CIRED Porto Workshop 2022: E-Mobility and Power Distribution Systems. doi: 10.1049/icp.2022.0712.

Torres-Olguin, R., S. Sanchez-Acevedo, O. Mo, and A. Garces-Ruiz (2023). Cyber-physical power system testing platform for topology identification in power distribution grids. IEEE Powertech 2023. doi: 10.1109/PowerTech55446.2023.10202733.

Uciński, D. (2000). Optimal sensor location for parameter estimation of distributed processes. International Journal of Control 73, 1235–1248. doi: 10.1080/002071700417876.

Uciński, D. (2012). Sensor network scheduling for identification of spatially distributed processes. International Journal of Applied Mathematics and Computer Science 22, 25–40. doi: 10.2478/v10006-012-0002-0.

Uciński, D. (2022). E-optimum sensor selection for estimation of subsets of parameters. Measurement 187, 110286. doi: 10.1016/j.measurement.2021.110286.

Varbella, A., B. Gjorgiev, and G. Sansavini (2023). Geometric deep learning for online prediction of cascading failures in power grids. Reliability Engineering & System Safety 237, 109341. doi: 10.1016/j.ress.2023.109341.

Verdier, G., N. Hilgert, and J.-P. Vila (2008). Optimality of CUSUM Rule Approximations in Change-Point Detection Problems: Application to Nonlinear State–Space Systems. IEEE Transactions on Information Theory 54, 5102–5112. doi: 10.1109/TIT.2008.929964.

Weng, Y., R. Negi, and M. D. Ilić (2019). Probabilistic joint state estimation for operational planning. IEEE Transactions on Smart Grid 10, 601–612. doi: 10.1109/TSG.2017.2749369.

Wu, X.-H. and S.-M. Song (2019). Robust information unscented particle filter based on M-estimate. IET Signal Processing 13, 14–20. doi: 10.1049/iet-spr.2018.5151.

Xygkis, T. C., G. N. Korres, and N. M. Manousakis (2018). Fisher Information-Based Meter Placement in Distribution Grids via the D-Optimal Experimental Design. IEEE Transactions on Smart Grid 9, 1452–1461. doi: 10.1109/TSG.2016.2592102.

Zamzam, A. S. and N. D. Sidiropoulos (2020). Physics-Aware Neural Networks for Distribution System State Estimation. IEEE Transactions on Power Systems 35, 4347–4356. doi: 10.1109/TPWRS.2020.2988352.

To top of page